A Standardized Exam Scores Are Normally Distributed

By Vi_Alani861 18 May, 2022 Post a Comment

Every z-score has an associated p-value that tells you the probability of all values below or. However standardized tests are designed sothat the outcome follows a normal distribution curve.

Solved A Standardized Exam S Scores Are Normally Chegg Com

Find the z-scores that correspond to each value and determine whether any of the values are unusual.

. A standardized exams scores are normally distributed. A standardized exams scores are normally distributed. Standard Normal Distribution.

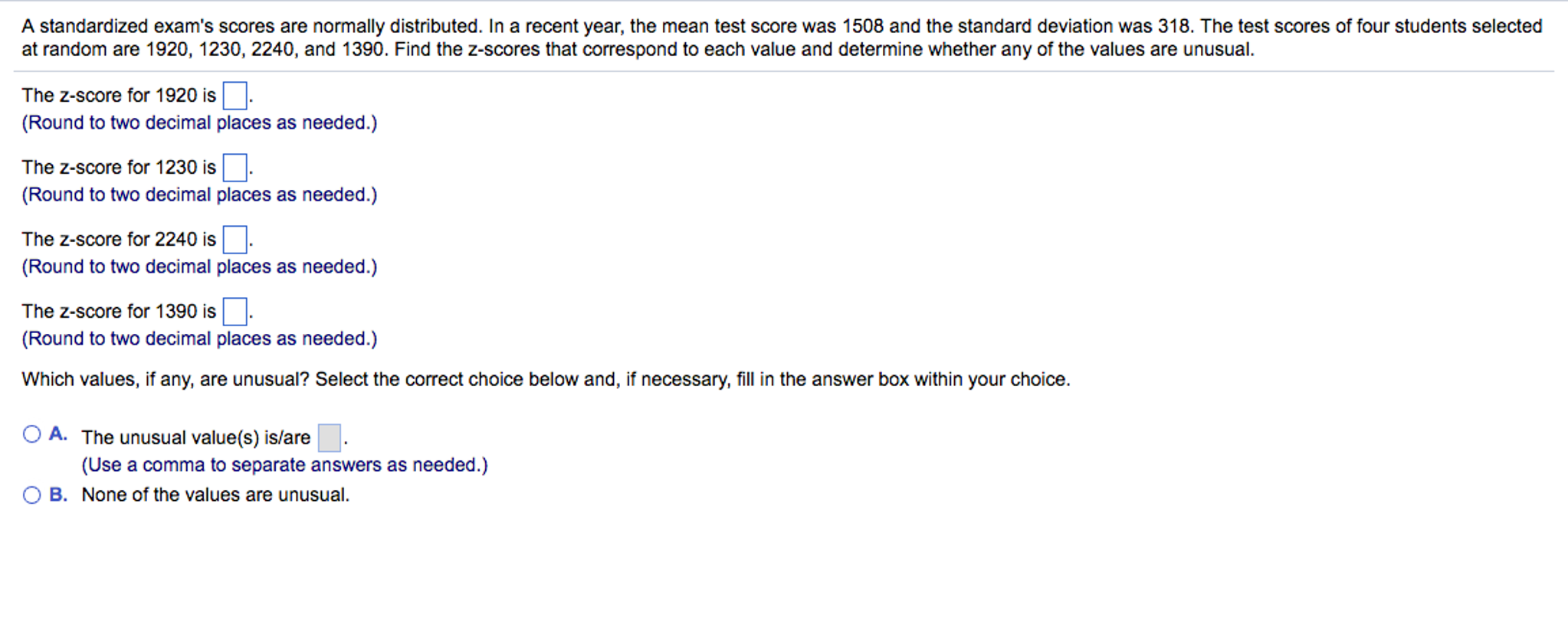
A standardized exams scores are normally distributed. Find the z-scores that correspond to each value and determine whether any of the values are unusual. In a recent year the mean test score was 1476 and the standard deviation was 320.

Find the Z-scores that correspond to each value and determine whether any of the values are unusual. Find the z-scores that correspond to each value and determine whether any of the values are unusual. A standardized exams scores are normally distributed.

The scores on a standardized exam are normally distributed with a. Its distribution is the standard normal Z N0 1. Theycan be skewed ie.

The scores on a standardized test for high school students are normally distributed with a population mean of 500 and a population standard deviation of 100. In a recent year. ABoth the mean and median score will equal 0.

A standardized exams scores are normally distributed. A standardized exams scores are normally distributed. The standard normal distribution is a special case of the normal distribution.

A standardized exams scores are normally distributed. The test scores of four students selected at random are 1910 1260 2200 and 1400_ Find the z-scores that correspond to each value and determine whether any of the values are unusual. Use the standard normal distribution to find probability.

A standardized exams scores are normally distributed. In a recent year the mean test score was 1469 and the standard deviation was 319. The Z-score for 1910 is Round to two decimal places.

Find the z-scores that correspond to each value and determine whether any of the values are unusual. So our normal distribution looks like this. The test scores of four studentsselected at random are 1920 1220 2220 and 1380.

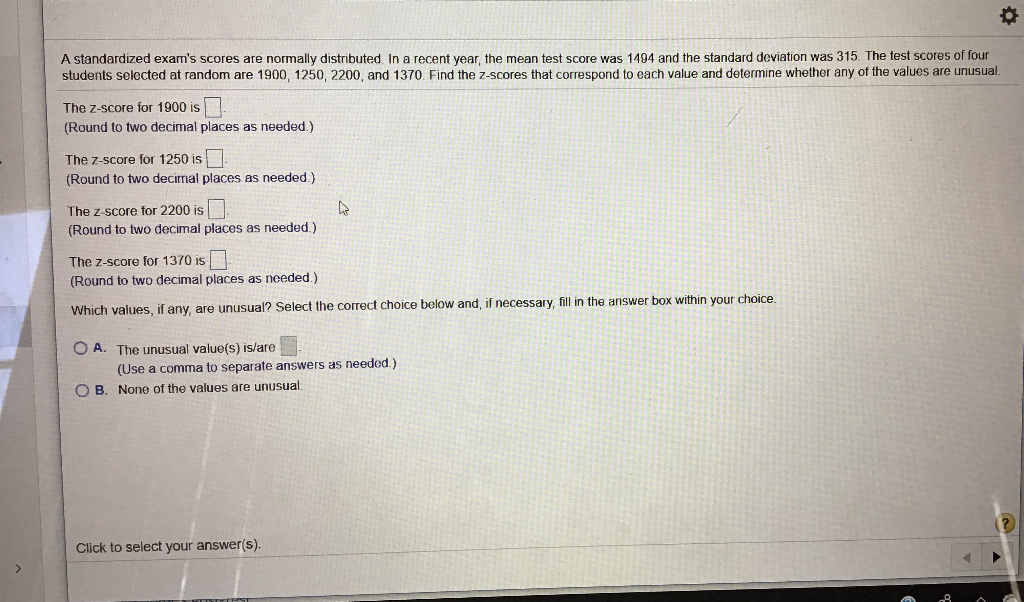
In a recent year the mean test score was 1507 and the standard deviation was 315. The data follows a normal distribution with a mean score M of 1150 and a standard deviation SD of 150. If these scores are converted to standard normal Z scores which of the following statements will be correct.

The scores on a standardized exam are normally distributed with a mean of 245 and a standard deviation of 54. The marks on a statistics test are normally distributed with a mean of 62 and a variance of 225. Suppose scores on an IQ test are normally distributed.

In a recent year the mean test score was 1548 and the standard deviation was 319. In a recent year the mean test score was 212 and the standard deviation was 57. A standardized exams scores are normally distributed.

The standard normal distribution is a probability distribution so the area under the curve between two points tells you the probability of variables taking on a range of valuesThe total area under the curve is 1 or 100. In a recent year the mean test score was 1503 and the standard deviation was 314 The test scores of four students selected at random are 1930 1220 2200 and 1380. A z-score is a standardized value.

BThe mean will equal 0 but the median cannot be determined. A standardized exams scores are normally distributed. The test scores of four students selected at random are 1890 1180 2210and 1350.

Solution for A standardized exams scores are normally distributed. It is the distribution that occurs when a normal random variable has a mean of zero and a standard deviation of one. Z N.

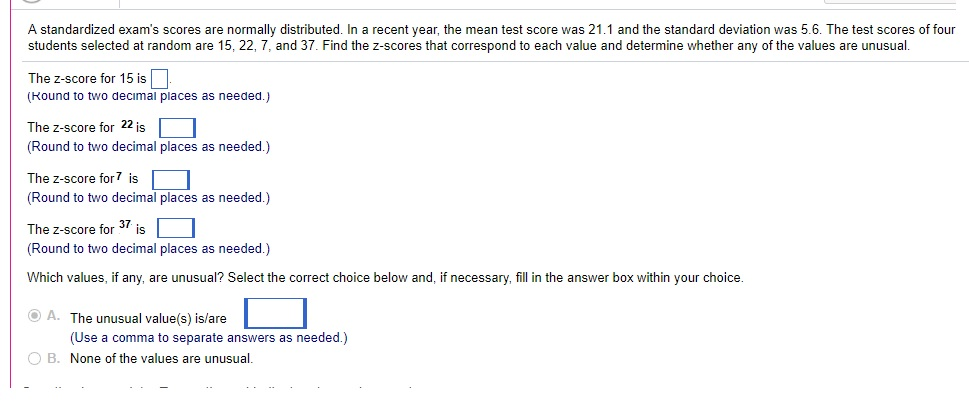
Scores on standardized Exam Y are normally distributed with mean 21 and standard deviation 5. Find the z-scores that correspond to each value and determine whether any of the values are unusual. The test scores of four students selected at random are 16 24 9 and 36.

The z-score for 1900 is nothing. In a recent year the mean test score was 1529 and the standard deviation was 320. Use technology or a z -score table to answer the questions.

The test scores of four students selected at random are 15 24 7 and 37. Using the empirical rule in a normal distribution You collect SAT scores from students in a new test preparation course. Find the z-scores that correspond to each value and determine whether any of the values are unusual.

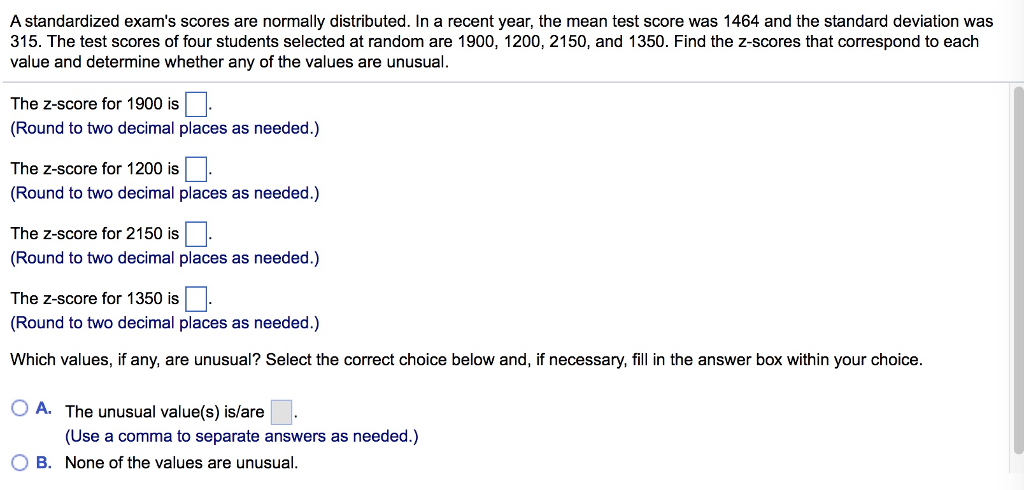
In a recent year the mean test score was 1462 and the standard deviation was 319. Find the z-scores that correspond to each value and determine whether any of the values are unusual. Have a disproportionate number of people who dovery well or very poorly.

If zis the z-score for a value x from the normal distribution Nµ σ then z tells you how many standard deviations x is above greater than or below less than µ. This would be the case if a test was too easy or toohard for the testing population. Following the empirical rule.

The mean of the z-scores is zero and the standard deviation is one. Find the z-scores that correspond to each value and determine whether any of the values are unusual. In a recent year the mean test score was 211 and the standard deviation was 57 The test scores of four students selected at random are 14 23 77 and 37 Find the z-scores that correspond to each value and determine whether any of the values are unusual.

Use the empirical rule 0LI refers to this as the standard deviation rule. Scores on a standardized test are normally distributed with a mean of 100 and a standard deviation of 20. The test scores of four students selected at random are 1900 1260 2220 and 1390.

Scores on standardized Exam X are normally distributed with mean 500 and standard deviation 100. Of course not all test score distributions are normally distributed. Find the z-scores that correspond to each value and determine whether any of the values are unusual.

In a recent year the mean test score was 214 and the standard deviation was 53. Bailey scored higher than 90 of all other people taking the exam. The test scores of four students selected at random are 15 22 8 and 36.

The test scores of four students selected at random are 1970 1280 2220 and 1410. At this point we can see that 16 of the values are greater than 600 So Quantity A 16 Given. If the test has a mean of 100 and a standard deviation of 10.

The mean test score was 1524 and the standard deviation was 310. The test scores of four students selected at random are 1990 1280 2240 and 1450. In a recent year the mean test score was 213 and the standard deviation was 55.

In a recent year the mean test score was 1527 and the standart deviation was 318The test scores of four students selected at random are 1970 1280 2250 1420. A standardized exams scores are normally distributed. A standardized exams scores are normally distributed.

Solved A Standardized Exam S Scores Are Normally Chegg Com